ناهم واریانسی چیست؟

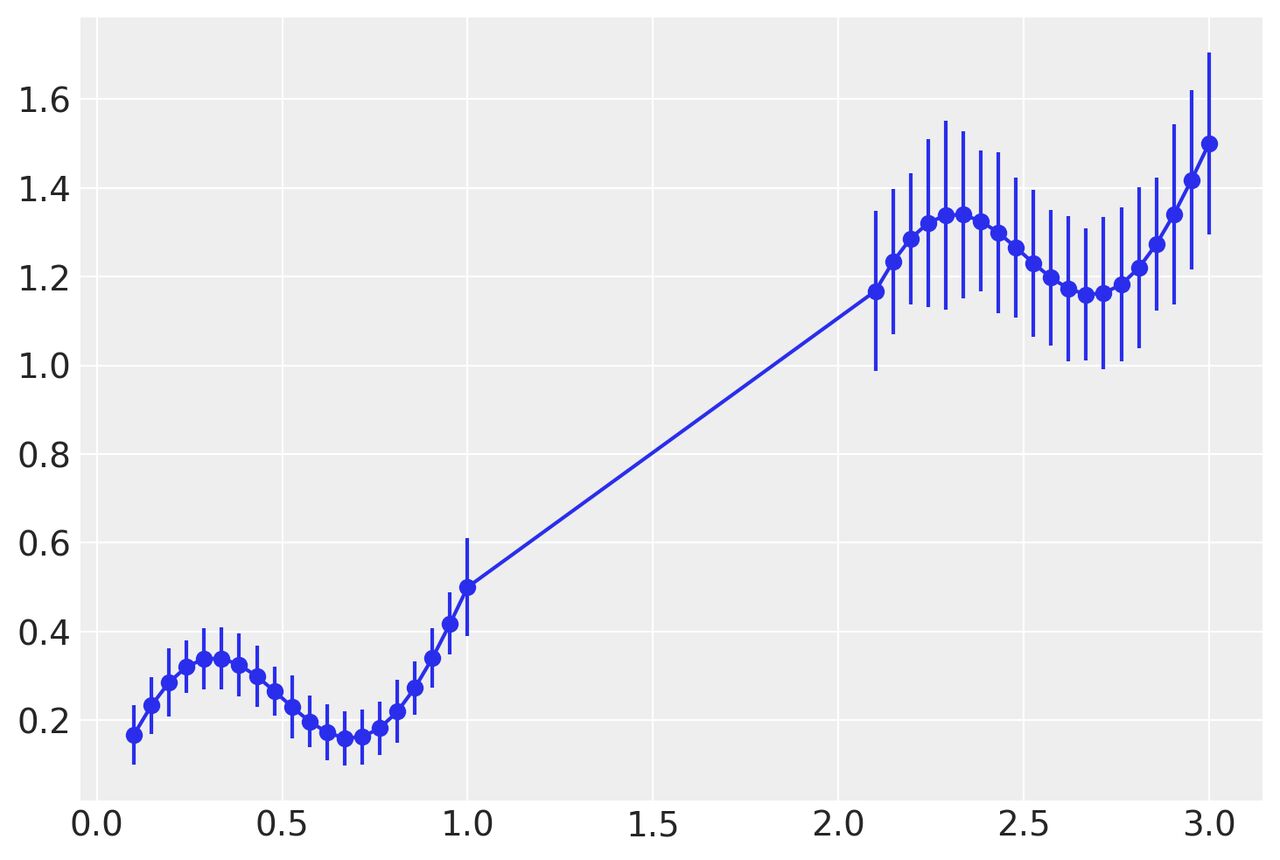
علامت مشخص ناهم واریانسی هنگام بازرسی بصری خطاهای باقیمانده این است که این خطاها به مرور زمان و همانطور که در تصویر زیر نشان داده شده است پراکنده می‌شوند.

ناهم واریانسی اغلب به دو شکل ظاهر می شود: مشروط و نامشروط. ناهم‌واریانسی مشروط، نوسانات متغیر مربوط به نوسانات دوره قبل (به عنوان مثال، روزانه) را مشخص می‌کند. ناهم واریانسی نامشروط به تغییرات ساختاری کلی در نوسانات اشاره دارد که به نوسانات دوره قبل مربوط نمی‌شوند. زمانی که دوره‌های آتی نوسانات بالا و پایین قابل شناسایی باشند، از ناهم واریانسی نامشروط استفاده می‌شود.

ناهم واریانسی

تصویر توسط جولی بنگ  اینستوپدیا 2019©

نکات کلیدی

• در آمار، ناهم واریانسی (یا ناهمگونی) زمانی اتفاق می‌افتد که هنگام پایش خطاهای استاندارد یک متغیر پایش در طول زمان، این خطاها ثابت نباشند.
• علامت مشخص ناهم واریانسی هنگام بازرسی بصری خطاهای باقیمانده این است که مطابق تصویر فوق، با گذشت زمان این خطاها پراکنده شوند.
• ناهم واریانسی تخطی از مفروضات مدل‌سازی رگرسیون خطی است و بنابراین ممکن است بر اعتبار تحلیل اقتصادسنجی یا مدل‌های مالی مانند CAPM تأثیر بگذارد.

مهم

در حالی که ناهم واریانسی باعث سوگیری در برآورد ضرایب نمی‌شود، اما دقت آن‌ها را کاهش می‌دهد. دقت کمتر ضرایب برآورد شده، احتمال انحراف بیشتر آن‌ها را از مقدار صحیح جمعیت افزایش می‌دهد.

مبانی ناهم واریانسی

در امور مالی، ناهم واریانسی مشروط اغلب در قیمت سهام و اوراق قرضه دیده می‌شود. سطح نوسانات این نوع سهم‌ها را نمی توان در هیچ دوره‌ای پیش بینی کرد. هنگام بحث در مورد متغیرهایی مانند مصرف برق که دارای تنوع فصلی قابل تشخیصی هستند، می‌توان از ناهم واریانسی نامشروط استفاده کرد.

تا آنجا که به آمار مربوط می‌شود، ناهم واریانسی (که همچنین به صورت heteroscedasticity نیز نوشته می‌شود) به واریانس خطا یا وابستگی پراکندگی در مقادیر حداقل یک متغیر مستقل در یک نمونه خاص اشاره دارد. این تغییرات را می‌توان برای محاسبه حاشیه خطا بین مجموعه داده‌ها، مانند نتایج مورد انتظار و نتایج واقعی، استفاده کرد زیرا معیاری از انحراف نقاط داده از مقدار متوسط را ارائه می‌دهند.

برای اینکه بتوان یک مجموعه داده را مهم در نظر گرفت، اکثر نقاط داده آن باید در فاصله تعداد معینی انحراف معیار از مقدار میانگین که توسط قضیه چبیشف توضیح داده شده است، که به نام نابرابری چبیشف نیز شناخته می‌شود، قرار داشته باشند. این قضیه دستورالعمل‌هایی را در مورد احتمال متفاوت بودن مقدار یک متغیر تصادفی از مقدار میانگین آن ارائه می‌دهد.

بر اساس تعداد انحرافات معیار تعیین شده، مقدار یک متغیر تصادفی به احتمال خاصی است در آن محدوده نقاط قرار خواهد گرفت. به‌عنوان مثال، ممکن است لازم باشد که محدوده‌ای به فاصله دو انحراف معیار حاوی حداقل 75 درصد از نقاط داده باشد تا نقاط داده معتبر در نظر گرفته شوند. یکی از دلایل رایج واریانس مقادیر متغیر به محدوده خارج از حداقل محدوده مورد نیاز، اغلب به مشکلات کیفیت داده‌ها مرتبط می‌شود.

نقطه مقابل ناهم‌واریانسی، هم‌واریانسی یا Homoskedasticity است. هم‌واریانسی به شرایطی اشاره دارد که در آن واریانس عبارت باقیمانده ثابت یا تقریباً ثابت است. هم‌واریانسی یکی از فرضیات مدل‌سازی رگرسیون خطی است. این فرضیه برای اطمینان از دقیق بودن تخمین‌ها، معتبر بودن محدودیت‌های پیش بینی برای متغیر وابسته و معتبر بودن بازه‌های اطمینان و مقادیر p پارامترها لازم است.

انواع ناهم‌واریانسی

نامشروط

ناهم‌واریانسی نامشروط قابل پیش بینی است و ممکن است به متغیرهایی مرتبط باشد که ماهیت چرخه‌ای دارند. این ناهم‌واریانسی ممکن است شامل گزارش آمار فروش بالاتر خرده‌فروشی‌ها در دوره‌های خرید تعطیلات متعارف یا افزایش تعداد تماس‌های مربوط به تعمیر کولر گازی در ماه‌های گرم‌تر سال باشد.

اگر تغییرات به طور متعارف فصلی نباشند، تغییرات واریانس را می‌توان به طور مستقیم به وقوع رویدادهای یا نشانگرهای پیش‌بینی‌کننده خاص نسبت داد. این تغییرات ممکن است به افزایش فروش گوشی‌های هوشمند با عرضه یک مدل جدید مرتبط باشند، زیرا این فعالیت بر اساس ماهیت رویداد ادواری به حساب می‌آید اما لزوماً دوره‌های آن بر اساس فصول تعیین نمی‌شوند.

ناهمواریانسی همچنین ممکن است به مواردی مربوط شود که در آن‌ها داده‌ها به یک مقدار مرزی نزدیک می‌شوند - که در آن واریانس باید لزوماً کوچکتر باشد زیرا این مقدار مرزی محدوده تغییر داده‌ها را محدود می‌سازد.

مشروط

ناهم‌واریانسی مشروط ماهیت قابل پیش‌بینی ندارد. هیچ نشانه‌ای وجود ندارد که تحلیلگران را به این باور برساند که پراکندگی داده‌ها در یک مقطع زمانی خاص کمتر یا بیشتر می‌شود. اغلب، محصولات مالی تابع ناهم‌واریانسی مشروط در نظر گرفته می‌شوند، زیرا نمی‌توان تمام تغییرات آن‌ها را به رویدادهای خاص یا تغییرات فصلی نسبت داد.

یکی از کاربردهای متداول ناهمگونی مشروط در بازارهای سهام است، جایی که نوسان امروز به شدت به نوسان دیروز مرتبط است. این مدل دوره‌های پر نوسان و کم نوسان را توضیح می‌دهد.

ملاحظات ویژه

ناهم‌واریانسی و مدل‌سازی مالی

ناهم‌واریانسی مفهومی مهم در مدل‌سازی رگرسیونی است و در دنیای سرمایه‌گذاری از مدل های رگرسیونی برای توضیح عملکرد اوراق بهادار و سبد سرمایه‌گذاری استفاده می‌شود. شناخته شده‌ترین آن‌ها مدل قیمت‌گذاری دارایی‌های سرمایه‌ای (CAPM) است که عملکرد سهام را بر حسب نوسانات آن نسبت به نوسانات کل بازار توضیح می‌دهد. در بسط‌های این مدل، متغیرهای پیش‌بینی‌کننده دیگری مانند اندازه، تکانه، کیفیت و سبک (ارزش در مقابل رشد) به مدل اضافه شده‌اند.

این متغیرهای پیش‌بینی‌کننده به این دلیل اضافه شده‌اند که واریانس متغیر وابسته را توضیح می‌دهند یا در محاسبات لحاظ می‌کنند. عملکرد سبد سرمایه‌گذاری توسط مدل CAPM توضیح داده می‌شود. به‌عنوان مثال، توسعه‌دهندگان مدل CAPM آگاه بودند که مدل آن‌ها نمی‌تواند یک ناهنجاری جالب را توضیح دهد: عملکرد سهم‌های با کیفیت بالا، که نوسانات کمتری نسبت به سهام کم‌کیفیت‌تر داشتند، بهتر از پیش‌بینی‌های مدل CAPM بود. مدل CAPM بیان می‌کند که عملکرد سهم‌های پرریسک‌تر باید بهتر از عملکرد سهم‌های کم‌ریسک‌تر باشد.

به‌عبارت دیگر، عملکرد سهم‌هایی پرنوسان‌تر باید بسیار بهتر از سهم‌هایی با نوسان کمتر باشد. اما در واقعیت، عملکرد سهم‌های با کیفیت بالا که نوسانات کمتری دارند، معمولا بهتر از پیش‌بینی‌های مدل CAPM بوده است.

بعداً، محققان دیگری مدل CAPM (که قبلاً برای شمول متغیرهای پیش‌بینی‌کننده دیگری مانند اندازه، سبک و تکانه گسترش یافته بود) را مجددا گسترش دادند تا کیفیت را نیز به‌عنوان یک متغیر پیش‌بینی‌کننده اضافی، که به عنوان «عامل» نیز شناخته می‌شود، در بر بگیرد. با در نظر گرفتن این عامل در این مدل، ناهنجاری عملکرد سهم‌های کم‌نوسان نیز توضیح داده شد. این مدل‌ها که به مدل‌های چند عاملی معروف هستند، اساس سرمایه‌گذاری عاملی و بتای هوشمند را تشکیل می‌دهند.