مجموع مربعات چیست؟ بررسی نحوه محاسبه آن
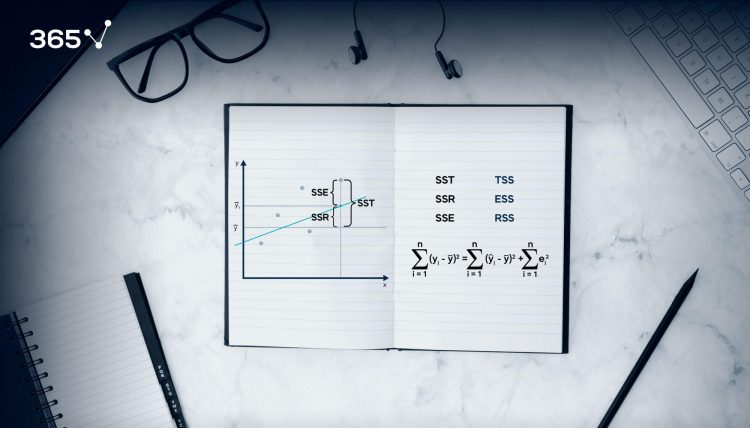
مجموع مربع ها انحراف نقاط داده را از مقدار میانگین اندازهگیری میکند.
از مجموع مربع ها می توان برای یافتن تابعی استفاده کرد که با کمترین تفاوت با داده ها با آنها مطابقت داشته باشد. هدف تجزیه و تحلیل بازگشتی تعیین نحوه برآزش بهینه یک مجموعه داده با تابعی است که ممکن است به توضیح نحوه تولید این مجموعه داده کمک کند. مجموع مربع ها را می توان در دنیای مالی برای تعیین واریانس ارزش دارایی ها استفاده کرد.
نکات کلیدی
مجموع مربعات بالاتر نشان دهنده تنوع بیشتر است در حالی که مجموع کمتر نشان دهنده تنوع کمتر نسبت به میانگین است.
برای محاسبه مجموع مربع ها، نقاط داده را از میانگین کم میکنند، سپس مربع نتایج را محاسبه رو آنها را با هم جمع میکنند.
سه نوع مجموع مربعها وجود دارد: مجموع کلی، باقیماندهها و بازگشتی.
سرمایه گذاران می توانند از مجموع مربع ها برای کمک به تصمیم گیری بهتر در زمینه سرمایه گذاری خود استفاده کنند.
معادله مجموع مربعات

آشنایی با مجموع مربع ها
مجموع مربعها معیاری آماری برای اندازهگیری انحراف از میانگین است. این معیار همچنین تنوع دادهها نیز شناخته می شود. این معیار با جمع کردن مجذور اختلاف هر نقطه داده از مقدار میانگین محاسبه می شود. برای تعیین مجموع مربع ها، مربع فاصله بین هر نقطه داده از خطی که بهترین برازش را با دادهها دارد محاسبه، سپس آنها را با هم جمع کنید. خطی که بهترین برازش را با دادهها دارد کمترین مقدار این معیار را به دست میدهد.
ارقام پایین مجموع مربع ها نشان دهنده تنوع اندک بین اعضای مجموعه داده است در حالی که ارقام بالاتر آن نشان دهنده تنوع بیشتر دادهها است. تنوع به تفاوت هر مجموعه داده از مقدار میانگین اشاره دارد. این مفهوم را میتوان بر روی نمودار تجسم کرد. اگر خط از تمام نقاط داده عبور نکند، تغییرات غیرقابل توضیحی وجود خواهد داشت. در بخش بعدی در زیر جزئیات بیشتری را در مورد این موضوع ارائه میکنیم.
تحلیلگران و سرمایه گذاران می توانند از مجموع مربع ها برای تصمیم گیری بهتر در مورد سرمایه گذاری خود استفاده کنند. بااینحال، به خاطر داشته باشید که استفاده از این معیار به معنای این است که بر اساس عملکرد گذشته قیمت مفروضاتی را ایجاد میکنید. به عنوان مثال، این معیار ممکن است در تعیین سطح نوسان قیمت سهام یا نحوه مقایسه قیمت سهام دو شرکت به شما کمک کند.
فرض کنید تحلیلگری می خواهد بداند آیا قیمت سهام مایکروسافت (MSFT) همگام با اپل (AAPL) حرکت می کند یا خیر، این فرد می تواند قیمت های روزانه هر دو سهم را در یک دوره معین (مثلاً یک، دو یا 10 سال) به ترتیب فهرست و یک مدل خطی یا نمودار برای آنها ایجاد کند. اگر رابطه بین هر دو متغیر (یعنی قیمت AAPL و MSFT) یک خط مستقیم نباشد، تغییراتی در مجموعه دادهها وجود دارد که باید به دقت بررسی شوند.
مهم
تنوع یک معیار آماری است که با استفاده از مجذور اختلاف مقادیر محاسبه یا اندازه گیری می شود.
نحوه محاسبه مجموع مربعات
تا به اینجا مشاهده کردید که چرا این معیار را مجموع مربعهای انحرافات یا به اختصار مجموع مربعات می نامند. برای محاسبه مجموع مربع ها می توانید از مراحل زیر استفاده کنید:
تمام نقاط داده را جمع آوری کنید.
میانگین یا مقدار متوسط را تعیین کنید.
میانگین/مقدار متوسط را از هر نقطه داده کسر کنید.
مربع هر مقدار حاصل برای هریک از دادهها در مرحله 3 را محاسبه کنید.
ارقام مرحله 4 را با یکدیگر جمع کنید.
مقدار میانگین در آمار، میانگین مجموعه ای از اعداد است که با جمع کردن مقادیر موجود در مجموعه داده ها و تقسیم عدد حاصل بر تعداد مقادیر محاسبه می شود. اما دانستن مقدار میانگین ممکن است برای تعیین مجموع مربع ها کافی نباشد. به این ترتیب، مقدار میانگین به تعیین دامنه تغییرات در مجموعهای از اندازهگیریها کمک میکند. میزان فاصله هریک از مقادیر از مقدار میانگین ممکن است بینشی در مورد تناسب مشاهدات یا مقادیر اندازهگیری شده با مدل رگرسیونی طراحی شده برای آنها ارائه دهد.
انواع مجموع مربعات
معادلهای که قبلاً به آن اشاره کردیم برای محاسبه مجموع مربعها استفاده می شود. مجموع کلی مجموع مربع ها برای محاسبه انواع دیگر این حاصلجمع استفاده می شود. در زیر انواع دیگری از مجموع مربع ها آورده شده است.
مجموع مربع های باقیماندهها
همانطور که در بالا ذکر شد، اگر خط ترسیم شده در مدل خطی از تمام مقادیر اندازهگیری شده عبور نکند، برخی از تغییراتی که در قیمتهای سهام مشاهده شده است غیرقابل توضیح خواهند بود. از مجموع مربع ها برای محاسبه وجود یا عدم وجود یک رابطه خطی بین دو متغیر استفاده می شود و هر تنوع غیرقابل توضیح به عنوان مجموع مربع ها باقیمانده نامیده می شود.
مجموع مربعهای باقیماندهها به شما اجازه می دهد تا میزان خطای باقیمانده بین یک تابع بازگشتی و مجموعه داده را پس از اجرای مدل تعیین کنید. میتوان ارقام کوچکتر مجموع مربعهای باقیمانده را به صورت برازش بهینه یک تابع بازگشتی با داده ها تفسیر کرد در حالی که عکس آن در مورد ارقام بزرگتر این معیار صادق است.
در اینجا معادله محاسبه مجموع مربع های باقیماندهها را ارائه میکنیم:

مجموع مربع های بازگشتی
مجموع مربع های بازگشتی برای نشان دادن رابطه بین داده های مدلسازی شده و یک مدل بازگشتی استفاده می شود. در این حالت برای تعیین وجود یا عدم وجود رابطه بین یک یا چند متغیر یک مدل بازگشتی تعیین میشود. مقادیر پایین مجموع مربعهای بازگشتی نشان دهنده برآزش بهتر مدل با داده ها است. با این حال، مقادیر بالاتر مجموع مربعهای بازگشتی به این معنی است که مدل و داده ها برآزش خوبی با یکدیگر ندارند.
در اینجا معادله محاسبه مجموع مربعهای بازگشتی را ارائه میکنیم:

نکته
جمع کردن مجموع انحرافات به تنهایی و بدون محاسبه مربع آنها عددی مساوی یا نزدیک به صفر را به دست میدهد، زیرا انحرافات منفی تقریباً به طور کامل انحرافات مثبت را خنثی خواهند کرد. برای به دست آوردن یک عدد واقعی تر، بایستی مجموع مربع انحرافات محاسبه شود. مجموع مربعات همیشه یک عدد مثبت خواهد بود زیرا مجذور هر عددی اعم از مثبت یا منفی همیشه مثبت است.
محدودیت های استفاده از مجموع مربع ها
تصمیم گیری در مورد سرمایه گذاری در خرید سهام نیازمند مشاهداتی بسیار بیشتر از آنچیزی است که در اینجا ذکر شد. ممکن است تحلیلگران برای حصول اطمینان بیشتر در مورد دامنه تغییرات قیمت یک دارایی مجبور شوند دادههای مربوط به سالهای زیادی را بررسی کنند. با اضافه شدن نقاط داده بیشتر به مجموعه، مجموع مربع ها بزرگتر می شود زیرا پراکندگی مقادیر بیشتر می شود.
پرکاربردترین معیارهای تغییرات، انحراف معیار و واریانس هستند. با این حال، برای محاسبه هر یک از این دو معیار، ابتدا باید مجموع مربع ها محاسبه شود. واریانس میانگین مجموع مربعات است (یعنی مجموع مربعهای مقادیر تقسیم بر تعداد مشاهدات). انحراف معیار نیز جذر واریانس است.
دو روش تحلیل بازگشتی وجود دارد که از مجموع مربعها در آنها استفاده میشود: روش حداقل مربعات خطی و روش حداقل مربعات غیرخطی. روش حداقل مربعات به این واقعیت اشاره دارد که تابع بازگشتی مجموع مربعات واریانس از نقاط داده واقعی را به حداقل می رساند. به این ترتیب می توان تابعی رسم کرد که از نظر آماری بهترین برآزش را با داده ها داشته باشد. توجه داشته باشید که یک تابع بازگشتی ممکن است خطی (یک خط مستقیم) یا غیر خطی (یک خط منحنی) باشد.
نمونه ای از مجموع مربع ها
اجازه بدهید از مایکروسافت به عنوان مثالی برای نمایش نحوه محاسبه مجموع مربعها استفاده کنیم.
با استفاده از مراحل ذکر شده در بالا، داده ها را جمع آوری می کنیم. بنابراین اگر بخواهیم عملکرد شرکت را در یک دوره پنج ساله بررسی کنیم، به قیمت های بسته شدن سهام آن در این بازه زمانی نیاز داریم:
$74.01
$74.77
$73.94
$73.61
$73.40
حالا اجازه بدهید میانگین قیمت آن را محاسبه کنیم. مجموع کل قیمت ها 369.73 دلار و میانگین یا مقدار متوسط قیمت $369.73 ÷ 5 = $73.95 میشود.
سپس مجموع مربع ها را محاسبه میکنیم، برای این کار ابتدا اختلاف هر قیمت را از میانگین پیدا و سپس مربع اختلاف مقادیر را محاسبه و آنها را با هم جمع می کنیم:

در مثال بالا، رقم 1.0942 نشان می دهد که تغییر در قیمت سهام MSFT در طول پنج روز بسیار پایین است و سرمایه گذارانی که به دنبال سرمایه گذاری در سهامی با ثبات قیمت و نوسانات پایین هستند، ممکن است سهام MSFT را انتخاب کنند.










