همبستگی چیست؟ نحوه محاسبه و فرمول آن
همبستگی آمارهای است که میزان ارتباط حرکت دو متغیر را نسبت به یکدیگر اندازه گیری می کند.
همبستگی ها در مدیریت پیشرفته سبد سرمایهگذاری استفاده و به صورت ضریب همبستگی محاسبه می شوند و مقدار آنها معمولا بایستی در بازه بین 1.0- و 1.0+ قرار بگیرد.
نکات کلیدی
در امور مالی، همبستگی می تواند حرکت یک سهام را نسبت به حرکت یک شاخص معیار مانند S&P 500 اندازه گیری کند.
همبستگی ارتباط نزدیکی با توزیع ریسک دارد، یعنی همان مفهومی که بیان میکند انواع مختلف ریسک را می توان با سرمایه گذاری در دارایی هایی که فاد همبستگی هستند کاهش داد.
همبستگی ارتباط بین دو متغیر را اندازه میگیرد، اما نشان نمیدهد که آیا x باعث y میشود یا برعکس – یا اینکه عامل سومی این ارتباط را ایجاد میکند یا خیر.
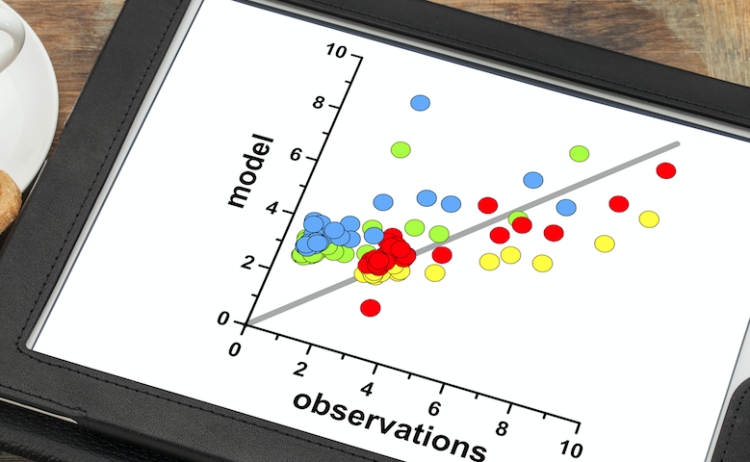
ممکن است تشخیص همبستگی با استفاده از نمودار پراکندگی آسانتر باشد، به خصوص اگر متغیرها همبستگی غیرخطی و در عین حال همچنان قوی داشته باشند.
همبستگی چه چیزی را به شما نشان میدهد
همبستگی قدرت رابطه بین دو متغیر را نشان می دهد و با ضریب همبستگی به صورت عددی بیان می شود. مقادیر ضریب همبستگی بین 1.0- و 1.0 متغیر هستند.
همبستگی مثبت کامل به این معنی است که مقدار ضریب همبستگی دقیقاً برابر 1 است. این مسئله نشان میدهد که با حرکت قیمت یک نوع اوراق بهادار به سمت بالا یا پایین، اوراق بهادار دیگری در همان جهت حرکت میکند. همبستگی منفی کامل به این معنی است که دو دارایی در جهت مخالف هم حرکت می کنند، در حالی که همبستگی صفر به این معنی است که هیچگونه رابطه خطی خاصی بین دو متغیر وجود ندارد.
به عنوان مثال، صندوقهای سرمایهگذاری بزرگ و معتبر معمولاً همبستگی مثبت بالا یا تقریباً برابر یک با شاخص استاندارد اند پورز (S&P) 500دارند. قیمت سهام شرکتهای کوچک نیز معمولاً همبستگی مثبتی با S&P دارند، اما مقدار ضریب همبستگی آنها چندان بالا نیست یا تقریباً برابر 0.8 است.
با این حال، قیمتهای قراردادهای اختیار فروش و قیمت سهام پایه آنها همبستگی منفی با یکدیگر دارند. اختیار فروش به مالک این قرارداد حق فروش مقدار مشخصی از اوراق بهادار پایه با قیمت از پیش تعیین شده را در یک بازه زمانی مشخص اعطا میکند اما وی را ملزم به انجام این کار نمیسازد.
قراردادهای اختیار فروش زمانی سودآورتر می شوند که قیمت سهام پایه کاهش یابد. به عبارت دیگر، با افزایش قیمت سهام، قیمت قرارداد اختیار فروش پایین میآید که یک همبستگی مستقیم و بزرگی منفی را نشان میدهد.
نحوه محاسبه همبستگی
روش های مختلفی برای محاسبه همبستگی وجود دارد. رایج ترین روش یعنی ضریب همبستگی گشتاوری پیرسون در این مقاله بیشتر مورد بحث قرار گرفته است. ضریب همبستگی گشتاوری پیرسون رابطه خطی بین دو متغیر را اندازه گیری می کند. از این ضریب میتوان برای هر مجموعه داده ای که ماتریس کوواریانس محدودی دارد، استفاده کرد. در اینجا مراحل محاسبه همبستگی آورده شده است.
داده ها متغیر «x» و«y» خود را جمع آوری کنید.
میانگین هر دو متغیر x و y را بیابید.
میانگین متغیر x را از هر مقدار متغیر x کم کنید. این مرحله را برای متغیر y نیز تکرار کنید.
هر اختلاف بین میانگین و مقدار متغیر x را در اختلاف متناظر مربوط به متغیر y ضرب کنید.
هر یک از این اختلاف را به توان 2 برسانید و نتایج را به یکدیگر اضافه کنید.
جذر مقدار بدست آمده در مرحله 5 را تعیین کنید.
مقدار مرحله 4 را بر مقدار بدست آمده در مرحله 6 تقسیم کنید.
مهم
برای جلوگیری از محاسبات دستی پیچیده، از تابع CORREL در اکسل استفاده کنید.
فرمول همبستگی
با استفاده از روش ضریب همبستگی گشتاوری پیرسون، می توان از فرمول زیر برای یافتن ضریب همبستگی r استفاده کرد:
که در آن:
r = ضریب همبستگی
n = تعداد مشاهدات
مثالی از همبستگی
محاسبه همبستگی برای مدیران سرمایهگذاری، معاملهگران و تحلیلگران بسیار مهم است زیرا مزایای کاهش ریسک ناشی از توزیع ریسک بر این آماره متکی است. صفحات گسترده و نرم افزارهای مالی می توانند مقدار همبستگی را به سرعت محاسبه کنند.
به عنوان یک مثال فرضی، فرض کنید که تحلیلگری بایستی همبستگی دو مجموعه داده زیر را محاسبه کند:
X: (41, 19, 23, 40, 55, 57, 33)
Y: (94, 60, 74, 71, 82, 76, 61)
برای یافتن همبستگی بایستی سه مرحله را طی کرد. اولین مرحله این است که تمام مقادیر X را برای یافتن (X) SUM و همه مقادیر Y را نیز برای پیدا کردن (Y) SUM بایستی با یکدیگر جمع کنید و هر مقدار X را در مقدار Y متناظر آن ضرب و مجموع آنها را برای یافتن (X,Y) SUM جمع کنید:
SUM(X) = (41 + 19 + 23 + 40 + 55 + 57 + 33) = 268
SUM(Y) = (94 + 60 + 74 + 71 + 82 + 76 + 61) = 518
SUM(X,Y) = (41 x 94) + (19 x 60) + (23 x 74) + … (33 x 61) = 20,391
مرحله بعدی این است که هر مقدار X را بگیرید، مربع آن را محاسبه میکند و تمام این مقادیر را برای یافتن (x^2) SUM با یکدیگر جمع کنید. همین کار را باید برای مقادیر Y انجام دهید:
SUM(X^2) = (41^2) + (19^2) + (23^2) + … (33^2) = 11,534
SUM(Y^2) = (94^2) + (60^2) + (74^2) + … (61^2) = 39174
با توجه به اینکه هفت مشاهده وجود دارد، n=7 از فرمول زیر می توان برای یافتن ضریب همبستگی r استفاده کرد:
که در آن:

r = ضریب همبستگی
n = تعداد مشاهدات
در این مثال، مقدار همبستگی برابر مقدار زیر خواهد بود:

همبستگی و توزیع ریسک سبد سرمایهگذاری
در حوزه سرمایه گذاری، همبستگی بیشترین اهمیت را در رابطه با توزیع ریسک سبد سرمایهگذاری دارد. سرمایه گذارانی که مایل به کاهش ریسک هستند می توانند با سرمایه گذاری در دارایی های غیر همبسته این کار را انجام دهند. به عنوان مثال، سرمایهگذاری را در نظر بگیرید که سهام شرکت هواپیمایی را خریداری کرده است. اگر مشخص شود که صنعت خطوط هوایی ارتباط کمی با صنعت رسانه های اجتماعی دارد، ممکن است این سرمایه گذار با درک اینکه اخبار منفی یک صنعت ممکن است بر صنعت دیگر تأثیر نداشته باشد، سرمایه گذاری در سهام رسانه های اجتماعی را انتخاب کند.
این رویکرد اغلب هنگام سرمایه گذاری در بین طبقات مختلف داراییها دنبال میشود. سهام، اوراق قرضه، فلزات گرانبها، املاک و مستغلات، ارزهای دیجیتال، کالاها و انواع دیگر سرمایه گذاری ها هر کدام روابط متفاوتی با یکدیگر دارند. در حالی که برخی از ابزارهای سرمایهگذاری ممکن است همبستگی بسیار بالایی به یکدیگر داشته باشند، برخی دیگر ممکن است فاقد همبستگی باشند و به عنوان پوشش ریسک برای تنوعبخشی به سبد سرمایهگذاری عمل کنند.
ریسکی که بتوان آن را توزیع کرد، ریسک غیر نظاممند نامیده می شود. این نوع ریسک مختص یک شرکت، صنعت یا طبقه دارایی خاص است. سرمایه گذاری در دارایی های مختلف می تواند همبستگی سبد سرمایهگذاری شما را کاهش دهد و میزان آسیبپذیری شما در برابر ریسکهای غیر نظاممند را کاهش دهد.
ملاحظات ویژه
همبستگی اغلب دیکته می شود و با سایر ملاحظات آماری مرتبط است. زمانی که از آمار برای تجزیه و تحلیل متغیرها استفاده می شود، معمولا به همبستگی اشاره میشود.
مقدار احتمال p
در آمار، از مقدار احتمال p برای نشان دادن معنادار بودن یا نبودن یافتهها به لحاظ آماری استفاده میشود. میتوان وجود همبستگی میان دو متغیر را نشان داد، اما ممکن است شواهد کافی برای بیان این ادعا به صورت یک ادعای قوی وجود نداشته باشد. مقدار p بالا نشان می دهد که شواهد کافی وجود دارد تا به طور معناداری نتیجه گرفت که ضریب همبستگی جمعیت مخالف صفر است.
نمودارهای پراکندگی
ساده ترین راه برای تجسم همبستگی دو متغیر این است که آنها را با استفاده از نمودار پراکندگی به صورت نموداری به تصویر بکشیم. هر نقطه در یک نمودار پراکندگی نشان دهنده یک مولفه از فضای نمونهای است. در نمودار پراکندگی، محور x یکی از متغیرهای مورد آزمایش را نشان می دهد، در حالی که محور y نشان دهنده متغیر دیگری است.
ضریب همبستگی دو متغیر اغلب برای نشان دادن رابطه دو متغیر به صورت یک خط راست در نمودار نشان داده می شود. اگر دو متغیر همبستگی مثبت داشته باشند، ممکن است خط راستی با شیب صعودی بر روی نمودار پراکندگی رسم شود. اگر دو متغیر همبستگی منفی داشته باشند، ممکن است خط راستی با شیب نزولی رسم شود. هرچه ارتباط نقاط داده قوی تر باشد، هر نقطه داده به این خط نزدیک تر خواهد بود.
از نمودارهای پراکندگی میتوان هنگام تجزیه و تحلیل داده های پیچیده تری که ممکن است روابط متغیری داشته باشند استفاده کرد. به عنوان مثال، ممکن است دو متغیر تا نقطه خاصی همبستگی مثبت داشته باشند، سپس همبستگی منفی پیدا کند. ممکن است شناسایی این رابطه غیر خطی با استفاده از فرمولها دشوارتر باشد اما زمانی که در نمودار پراکندگی ترسیم میشود، تشخیص آن آسانتر خواهد بود.
در نهایت، زمانی که از سایهزنی تراکم در نمودارهای پراکندگی استفاده میشود این نمودارها می توانند همبستگی متغیرها را به راحتی به تصویر بکشند. سایه چگالی یا بیضی چگالی ناحیهای سایهزنی شدهای روی نمودار پراکندگی است که متراکمترین ناحیه از نقاط داده را به صورت بصری بر روی نمودار نشان میدهد. اگر متغیرها مرتبط باشند، بیضیهای چگالی اغلب جهت خطوط همبستگی خطی را منعکس میکنند. در غیر این صورت، بیضیهای چگالی بیشتر شکل دایرهای پیدا میکنند و جهت مشخصی ندارند و همبستگی کمتری را نشان میدهند.
علیت
یکی دیگر از مشکلات ذاتی آمار، تعیین این مسئله است که آیا روابط بین دو متغیر از خود آن متغیرها ناشی شده است یا خیر. به عبارت زیر توجه کنید:
«بیشتر بازیکنان بسکتبال قد بلندی دارند. بنابراین اگر بسکتبال بازی کنید، قد بلند خواهید شد.»
واضح است که گفته بالا درست نیست. افرادی که قد بلندی دارند و این مزیت خود را درک می کنند ممکن است به بسکتبال گرایش پیدا کنند زیرا توانایی های فیزیکی طبیعی آنها تناسب بالایی با این ورزش دارد. با این حال، از آنجا که ممکن است قد و فعالیت در بسکتبال همبستگی مثبت داشته باشند، آماردانان و متخصصان علم داده باید توجه داشته باشند که رابطه قوی بین دو متغیر ممکن است به دلیل هر یک از این متغیرها ایجاد شود یا نشود.









